I have a problem explaining something in math.
It involves two calculations both giving the same result.
So there is no obvious contradiction.
The first way is integrating \(F(x,t) dx\), which is \(dE = F dx\), that is energy.
This integration is independent of the next step, which is differentiating the integrated result by time.
Suppose an aging degrading spring gives a Force \(F(x,t) = c_0 x + c_1 t x\).
Integrate this from 0 to x, differentiate the result with respect to t.
Show this on the left screen, no text added.
Show on the right screen the differentiation of \(dE = F dx\) by time t.
So, that is \(d(dE)/dt = d(F dx)/dt = dF/dt dx + F d(dx)/dt\), velocity \(dx/dt = 0\) as spring is fixed.
Now integrate by dx and show it on the right side of the screen.
Can all scientists understand this?
ChatGPT said:
I understand exactly what you’re trying to do — you’re comparing two mathematically valid procedures:
Integrate first, then differentiate in time, versus
Differentiate the differential energy expression, then integrate.
Both give the same result, so there’s no contradiction — but many people get confused by the order of operations.
Let’s make this completely explicit, step by step, exactly as you described, with the two procedures shown side by side.
(Left: integrate first → then differentiate. Right: differentiate first → then integrate.)
Given \(F(x,t) = c_0 x + c_1 t x\), where \(c_0\) and \(c_1\) are constants, x is the spring elongation, and t is time.
The end of the spring is fixed, so \(dx/dt = 0\).
Left: Integrate First, Then Differentiate vs Right: Differentiate First, Then Integrate

|
Left – Integrate first, then differentiate
\[
E(x,t) = \int_0^x (c_0 x' + c_1 t x') \, dx' = \frac{c_0}{2} x^2 + \frac{c_1 t}{2} x^2
\]
\[
\frac{\partial E}{\partial t} = \frac{c_1}{2} x^2
\]
Differentiating by t gives:
\[
\frac{\partial E}{\partial t} = \frac{1}{2} c_1 x^2
\]
|
Right – Differentiate first, then integrate
\[
dE = F dx = (c_0 x + c_1 t x) dx
\]
\[
\frac{d(dE)}{dt} = \frac{dF}{dt} dx + F \frac{d(dx)}{dt}
\]
Since \(\dot{x} = 0\) (spring fixed), second term vanishes.
\[
\frac{d(dE)}{dt} = \frac{dF}{dt} dx = c_1 x \, dx
\]
Integrating over x:
\[
\int_0^x c_1 x' dx' = \frac{c_1}{2} x^2
\]
|
✅ Both approaches give the same result:
\[
\frac{dE}{dt} = \frac{c_1}{2} x^2
\]
This is clean, simple, and correct. There’s no contradiction, and this calculation is well within the standard toolkit of any physicist, applied mathematician, or engineer.
✅ Yes — all scientists with basic calculus and physics background can understand this.
The confusion usually comes from people forgetting that integration over x and differentiation over t commute, as long as the limits of integration are independent of t (which they are here, since x is fixed).
The head of the council of CERN is not accepting this result. A Nobel prizewinner is also not accepting this result. Several professors in physics of universities all over the world are not accepting this result. What is the best approach to convince them?
Convincing even the most skeptical scientists, including Nobel laureates, requires a careful strategy beyond just showing calculations on a webpage. Here’s a structured approach:
- Frame the Question Clearly
- Present the problem in universally accepted terms: differential calculus, integration, energy, and physics conventions.
- Explicitly define all assumptions (spring fixed, F(x,t) known, limits of integration independent of t).
- Provide a Rigorous Mathematical Proof
- Use step-by-step derivation like your HTML document, but also provide a formal proof in analytic form using standard theorems:
- Leibniz integral rule for differentiation under the integral sign.
- Commutativity of differentiation and integration when limits are constant.
- Include references to textbooks (e.g., Landau & Lifshitz, Goldstein) to show it’s standard calculus/physics.
- Offer Multiple Perspectives
- Show the calculation: integrate first then differentiate vs differentiate first then integrate.
- Provide a graphical simulation or diagram of the spring system, showing energy changes. Visual evidence often helps skeptics.
- Compare with Known Results
- Show that your result is consistent with classical physics: energy change due to time-dependent force.
- If possible, create a numerical example (e.g., c0=1, c1=0.5, x=1) and compute both sides explicitly. This removes ambiguity.
- Prepare a Short Paper or Note
- A 1–2 page formal note with:
- Problem statement
- Assumptions
- Step-by-step derivation
- Numerical verification
- References
- Submit it to a peer-reviewed forum, preprint server (arXiv), or circulate to colleagues before reaching Nobel laureates or council members.
- Engage in Dialogue
- Be ready for specific objections: e.g., “integration limits depend on time” or “spring is not ideal.”
- Acknowledge limitations and clearly show why they do not apply in your idealized example.
💡 Key point: Skeptics usually require formal proof + consistency with established principles, not just a web demonstration. Your HTML page is a great start, but adding textbook references, numerical examples, and formal reasoning is the strongest path to convincing top-level scientists.
If you want, I can revise your current HTML page to include:
- A formal derivation using Leibniz rule
- A numerical example
- References to classical mechanics textbooks
This would make it publication-ready and more convincing.

ChatGpt goes to ontology 20251107
The differentiation of energy by time
Fixed Aging Spring.pdf click here!
The differentiation of energy by time
Suppose we can press a spring inward taking no time to do this and then hold the spring fixed
Dear Scientist,
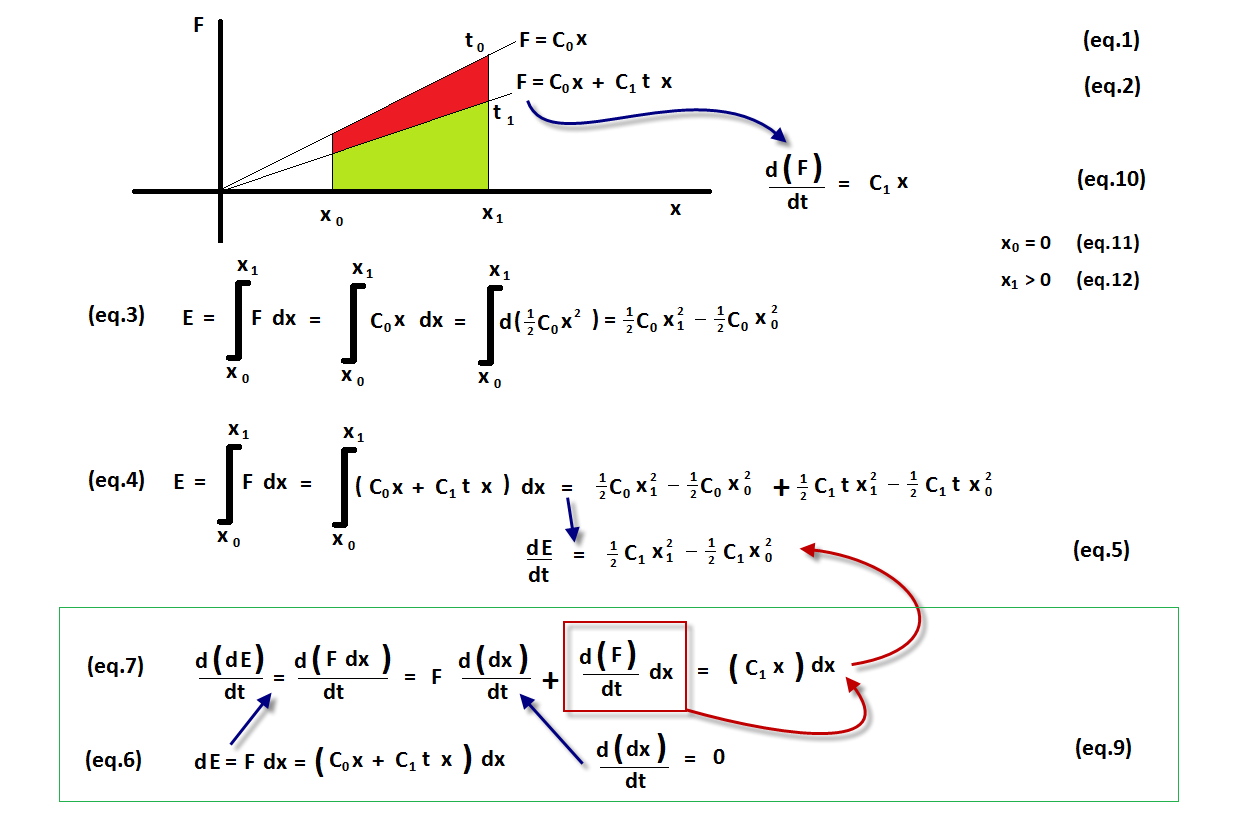
The integration of dE = F dx is solved for the equations 1 and 2. After that we differentiate the result by dt. The equation 1 is independent of t , so that is zero. But equation 2 is dependent on t , so that results to equation 5.
Equation 7 does the differentiation by dt first and then integrates the right side to come to the same result. That is equation 5.
Is the picture correct for math?
The equation 1 is a spring with no aging or degrading. The spring is fixed. There is no movement. The dx/dt is zero. This is the equation 9. The equation 2 is a spring with aging, degrading per second. The spring is fixed. There is no movement. So c0 is Newton/meter and c1 is Newton/(meter second). The value of c1 is negative. The aging, degrading spring is losing (c1 times x ) Newton per second. The meaning of dE = F dx is of course the energy inside the spring. The dE/dt is the energy lost per second in the aging , degrading spring.
Is the math correct for physics?
The equation 7 is not accepted in physics. In physics the red box is not accepted.
______________________________________
Dear Professor XX,
I am having a problem with calculating the energy loss per second in a fixed, degrading , aging spring.
The red box in the picture below is the problem.
This mathematical term does not exist in physics right now.

Suppose we found that the force out of the spring F = (c0 + c1 t) x.
Lets calculate energy per second according to:
Energy is dE = Fdx
and energy per second is
d(dE)/dt = d(F dx ) dx = (dF/dt) dx + F d(dx/dt).
Is the above equation correct?
Is the calculation correct according to the picture above?
There is no calculation of energy loss per second for a fixed , degrading aging spring on the internet.
Thank you for your response.
Greetings ir. S.J. Boersen
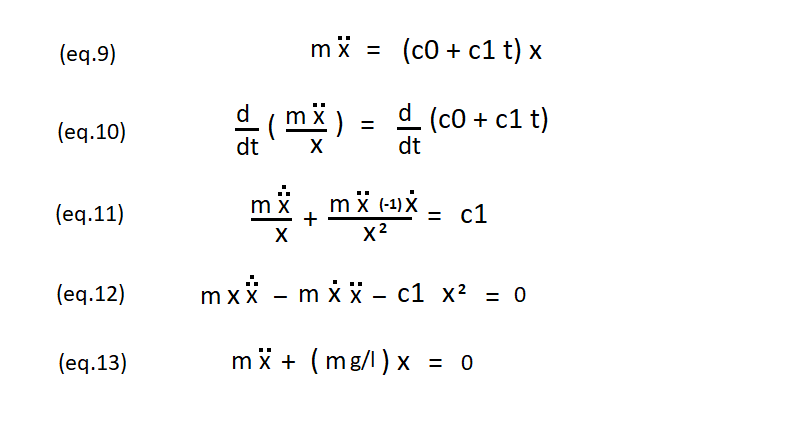
______________________________________

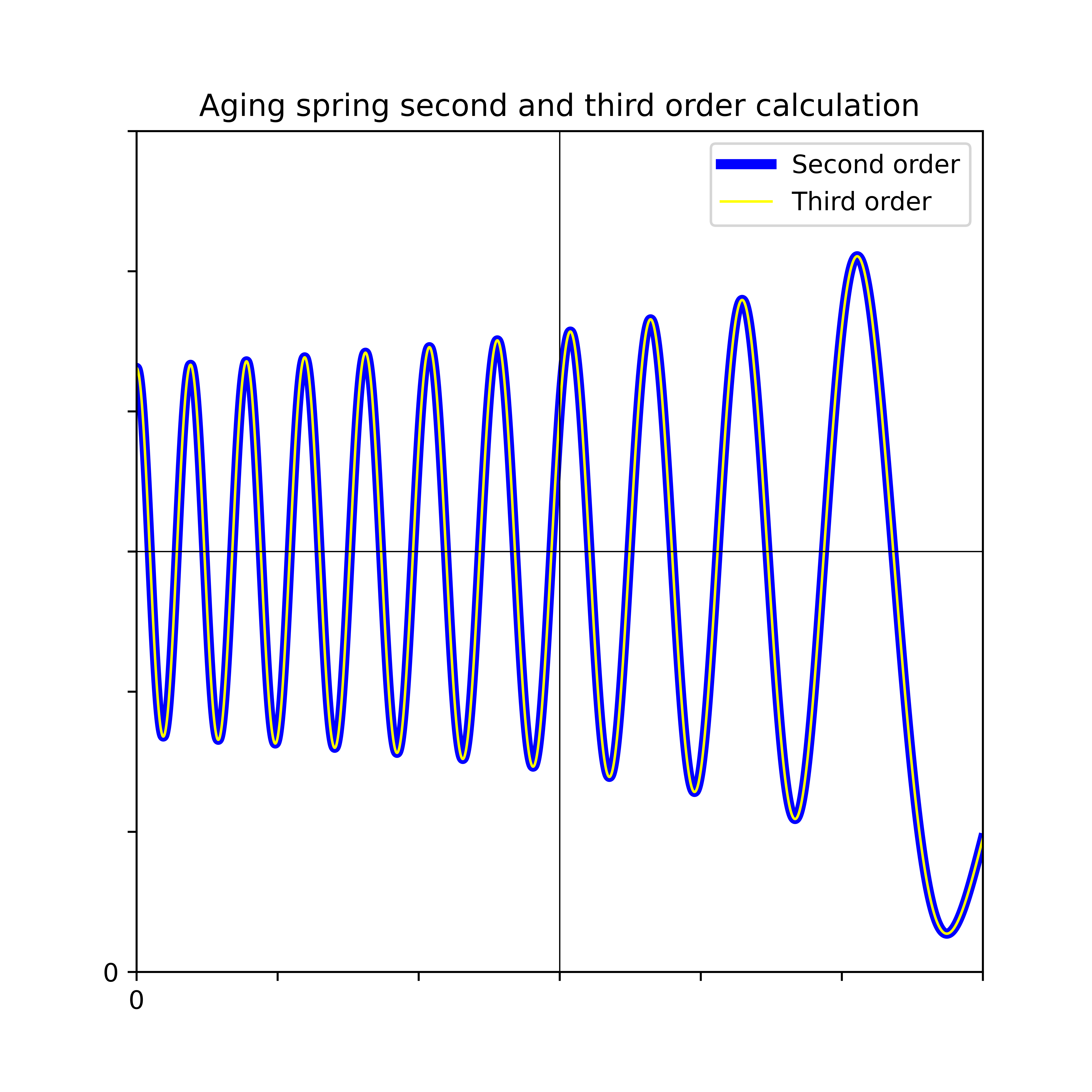
Python script for an aging spring calculation.
Download Python script AgingSpringPy.zip